I thought the muscular guys were supposed to be right in these memes.
He is right. 1 approximates 1 to any accuracy you like.
Is it true to say that two numbers that are equal are also approximately equal?
I recall an anecdote about a mathematician being asked to clarify precisely what he meant by “a close approximation to three”. After thinking for a moment, he replied “any real number other than three”.
“Approximately equal” is just a superset of “equal” that also includes values “acceptably close” (using whatever definition you set for acceptable).
Unless you say something like:
a ≈ b ∧ a ≠ b
which implies a is close to b but not exactly equal to b, it’s safe to presume that a ≈ b includes the possibility that a = b.
Can I get a citation on this? Because it doesn’t pass the sniff test for me. https://en.wikipedia.org/wiki/Approximation
Sure! See ISO-80000-2
Here’s a link: https://cdn.standards.iteh.ai/samples/64973/329519100abd447ea0d49747258d1094/ISO-80000-2-2019.pdf
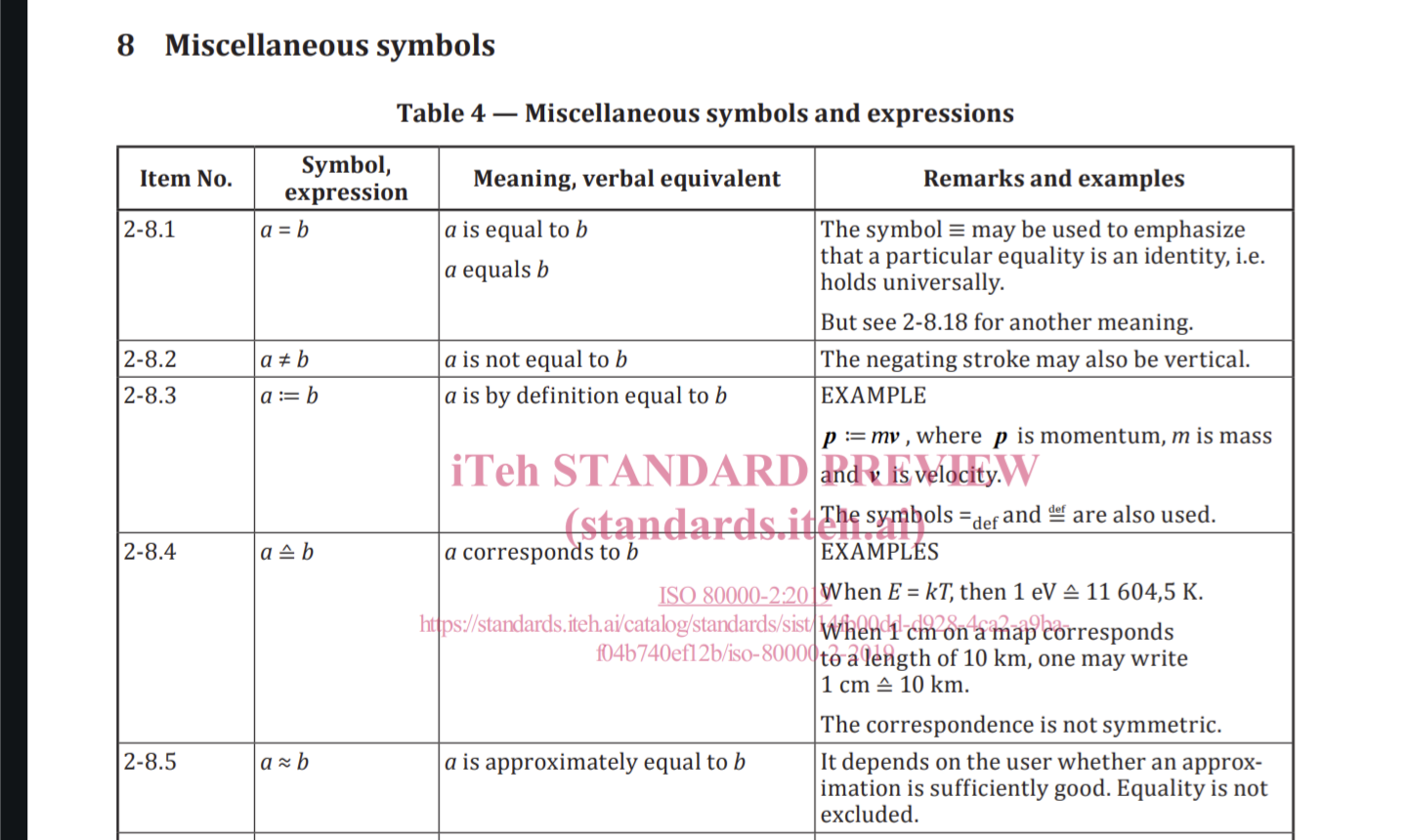
ISO is not a source for mathematical definitions
It’s a definition from a well-respected global standards organization. Can you name a source that would provide a more authoritative definition than the ISO?
There’s no universally correct definition for what the ≈ symbol means, and if you write a paper or a proof or whatever, you’re welcome to define it to mean whatever you want in that context, but citing a professional standards organization seems like a pretty reliable way to find a commonly-accepted and understood definition.
Yes, informally in the sense that the error between the two numbers is “arbitrarily small”. Sometimes in introductory real analysis courses you see an exercise like: “prove if x, y are real numbers such that x=y, then for any real epsilon > 0 we have |x - y| < epsilon.” Which is a more rigorous way to say roughly the same thing. Going back to informality, if you give any required degree of accuracy (epsilon), then the error between x and y (which are the same number), is less than your required degree of accuracy
Nah. They are supposed to not care about stuff and just roll with it without any regrets.
It’s just like the wojak crying with the mask on, but not crying behind it.
There’s plenty of cases of memes where the giga chad is just plainly wrong, but they just don’t care. But it’s not supposed to be in a troll way. The giga chad applies what it believes in. If you want a troll, there’s troll face, who speak with the confidence of a giga chad, but know he is bullshiting
0.9<overbar.> is literally equal to 1
There’s a Real Analysis proof for it and everything.
Basically boils down to
- If 0.(9) != 1 then there must be some value between 0.(9) and 1.
- We know such a number cannot exist, because for any given discrete value (say 0.999…9) there is a number (0.999…99) that is between that discrete value and 0.(9)
- Therefore, no value exists between 0.(9) and 1.
- So 0.(9) = 1
Even simpler: 1 = 3 * 1/3
1/3 =0.333333…
1/3 + 1/3 + 1/3 = 0.99999999… = 1
Even simpler
0.99999999… = 1
But you’re just restating the premise here. You haven’t proven the two are equal.
1/3 =0.333333…
This step
1/3 + 1/3 + 1/3 = 0.99999999…
And this step
Aren’t well-defined. You’re relying on division short-hand rather than a real proof.
ELI5
Mostly boils down to the pedantry of explaining why 1/3 = 0.(3) and what 0.(3) actually means.
That actually makes sense, thank you.
the explanation (not proof tbf) that actually satisfies my brain is that we’re dealing with infinite repeating digits here, which is what allows something that on the surface doesn’t make sense to actually be true.
Infinite repeating digits produce what is understood as a Limit. And Limits are fundamental to proof-based mathematics, when your goal is to demonstrate an infinite sum or series has a finite total.
This is why we can’t have nice things like dependable protection from fall damage while riding a boat in Minecraft.
Remember when US politicians argued about declaring Pi to 3?
Would have been funny seeing the world go boink in about a week.
I prefer my pi to be in duodecimal anyway. 3.184809493B should get you to where you need to go.
Some software can be pretty resilient. I ended up watching this video here recently about running doom using different values for the constant pi that was pretty nifty.
Reals are just point cores of dressed Cauchy sequences of naturals (think of it as a continually constructed set of narrowing intervals “homing in” on the real being constructed). The intervals shrink at the same rate generally.
1!=0.999 iff we can find an n, such that the intervals no longer overlap at that n. This would imply a layer of absolute infinite thinness has to exist, and so we have reached a contradiction as it would have to have a width smaller than every positive real (there is no smallest real >0).
Therefore 0.999…=1.
However, we can argue that 1 is not identity to 0.999… quite easily as they are not the same thing.
This does argue that this only works in an extensional setting (which is the norm for most mathematics).
deleted by creator
Thanks for the bedtime reading!
I mostly deal with foundations of analysis, so this could be handy.
Are we still doing this 0.999… thing? Why, is it that attractive?
Meh, close enough.
I wish computers could calculate infinity
Mathematics is built on axioms that have nothing to do with numbers yet. That means that things like decimal numbers need definitions. And in the definition of decimals is literally included that if you have only nines at a certain point behind the dot, it is the same as increasing the decimal in front of the first nine by one.
That’s not how it’s defined. 0.99… is the limit of a sequence and it is precisely 1. 0.99… is the summation of infinite number of numbers and we don’t know how to do that if it isn’t defined. (0.9 + 0.09 + 0.009…) It is defined by the limit of the partial sums, 0.9, 0.99, 0.999… The limit of this sequence is 1. Sorry if this came out rude. It is more of a general comment.
I study mathematics at university and I remember it being in the definition, but since it follows from the sum’s limit anyways it probably was just there for claritie’s sake. So I guess we’re both right…
0.(9)=0.(3)*3=1/3*3=1
deleted by creator
I think the … here is meant to represent repeating digits.
deleted by creator
Even the hyperreal numbers *R, which include infinitesimals, define 1 == .999…
Okay, but it equals one.
No, it equals 0.999…
2/9 = 0.222… 7/9 = 0.777…
0.222… + 0.777… = 0.999… 2/9 + 7/9 = 1
0.999… = 1
No, it equals 1.
Sure, when you start decoupling the numbers from their actual values. The only thing this proves is that the fraction-to-decimal conversion is inaccurate. Your floating points (and for that matter, our mathematical model) don’t have enough precision to appropriately model what the value of 7/9 actually is. The variation is negligible though, and that’s the core of this, is the variation off what it actually is is so small as to be insignificant and, really undefinable to us - but that doesn’t actually matter in practice, so we just ignore it or convert it. But at the end of the day 0.999… does not equal 1. A number which is not 1 is not equal to 1. That would be absurd. We’re just bad at converting fractions in our current mathematical understanding.
Edit: wow, this has proven HIGHLY unpopular, probably because it’s apparently incorrect. See below for about a dozen people educating me on math I’ve never heard of. The “intuitive” explanation on the Wikipedia page for this makes zero sense to me largely because I don’t understand how and why a repeating decimal can be considered a real number. But I’ll leave that to the math nerds and shut my mouth on the subject.
Similarly, 1/3 = 0.3333…
So 3 times 1/3 = 0.9999… but also 3/3 = 1Another nice one:
Let x = 0.9999… (multiply both sides by 10)
10x = 9.99999… (substitute 0.9999… = x)
10x = 9 + x (subtract x from both sides)
9x = 9 (divide both sides by 9)
x = 1My favorite thing about this argument is that not only are you right, but you can prove it with math.
Except it doesn’t. The math is wrong. Do the exact same formula, but use .5555… instead of .9999…
Guess it turns out .5555… is also 1.
Lol you can’t do math apparently, take a logic course sometime
Let x=0.555…
10x=5.555…
10x=5+x
9x=5
x=5/9=0.555…
you can prove it with math
Not a proof, just wrong. In the “(substitute 0.9999… = x)” step, it was only done to one side, not both (the left side would’ve become 9.99999), therefore wrong.
Sort of how 0.0000001 = 0
No, not like that.
x=.9999…
10x=9.9999…
Subtract x from both sides
9x=9
x=1
There it is, folks.
Somehow I have the feeling that this is not going to convince people who think that 0.9999… /= 1, but only make them madder.
Personally I like to point to the difference, or rather non-difference, between 0.333… and ⅓, then ask them what multiplying each by 3 is.
I’d just say that not all fractions can be broken down into a proper decimal for a whole number, just like pie never actually ends. We just stop and say it’s close enough to not be important. Need to know about a circle on your whiteboard? 3.14 is accurate enough. Need the entire observable universe measured to within a single atoms worth of accuracy? It only takes 39 digits after the 3.
The problem is, that’s exactly what the … is for. It is a little weird to our heads, granted, but it does allow the conversion. 0.33 is not the same thing as 0.333… The first is close to one third. The second one is one third. It’s how we express things as a decimal that don’t cleanly map to base ten. It may look funky, but it works.
pi isn’t even a fraction. like, it’s actually an important thing that it isn’t
I was taught that if 0.9999… didn’t equal 1 there would have to be a number that exists between the two. Since there isn’t, then 0.9999…=1
Divide 1 by 3: 1÷3=0.3333…
Multiply the result by 3 reverting the operation: 0.3333… x 3 = 0.9999… or just 1
0.9999… = 1
You’re just rounding up an irrational number. You have a non terminating, non repeating number, that will go on forever, because it can never actually get up to its whole value.
1/3 is a rational number, because it can be depicted by a ratio of two integers. You clearly don’t know what you’re talking about, you’re getting basic algebra level facts wrong. Maybe take a hint and read some real math instead of relying on your bad intuition.
1/3 is rational.
.3333… is not. You can’t treat fractions the same as our base 10 number system. They don’t all have direct conversions. Hence, why you can have a perfect fraction of a third, but not a perfect 1/3 written out in base 10.
0.333… exactly equals 1/3 in base 10. What you are saying is factually incorrect and literally nonsense. You learn this in high school level math classes. Link literally any source that supports your position.
.333… is rational.
at least we finally found your problem: you don’t know what rational and irrational mean. the clue is in the name.
TBH the name is a bit misleading. Same for “real” numbers. And oh so much more so for “normal numbers”.
not really. i get it because we use rational to mean logical, but that’s not what it means here. yeah, real and normal are stupid names but rational numbers are numbers that can be represented as a ratio of two numbers. i think it’s pretty good.
non repeating
it’s literally repeating
In this context, yes, because of the cancellation on the fractions when you recover.
1/3 x 3 = 1
I would say without the context, there is an infinitesimal difference. The approximation solution above essentially ignores the problem which is more of a functional flaw in base 10 than a real number theory issue
The context doesn’t make a difference
In base 10 --> 1/3 is 0.333…
In base 12 --> 1/3 is 0.4
But they’re both the same number.
Base 10 simply is not capable of displaying it in a concise format. We could say that this is a notation issue. No notation is perfect. Base 10 has some confusing implications
They’re different numbers. Base 10 isn’t perfect and can’t do everything just right, so you end up with irrational numbers that go on forever, sometimes.